티스토리 뷰
이 글은 그냥 개인적으로 공부한 내용을 정리할 목적으로 작성이 되었습니다 ㅎㅎ
마르코프 결정과정 (MDP) 관련 학습 내용
- 마르코프 연쇄 (Markov Chain)
- 마르코프 보상과정 (Markov Reward Process)
- 마르코프 결정과정 (Markov Decision Process)
마르코프의 특성
- 현재 상태에는 과거의 모든 정보가 포함되어 있다.
- 현재 상태를 알면 과거와 무관하게 미래상태를 예측할 수 있다.
마르코프 연쇄와 상태 변이 행렬(State Transition Matrix)
- 특정 상태에서 다른 상태로 변이될 확률을 표현한 행렬

| 집 | 학교 | 학원 | PC방 | 치킨 | 분식 | 피자 | 운동 | 만화 | 잠 | |
| 집 | 0.6 | 0.3 | 0.1 | |||||||
| 학교 | 0.3 | 0.4 | 0.3 | |||||||
| 학원 | 0.1 | 0.2 | 0.2 | 0.5 | ||||||
| PC방 | 0.2 | 0.8 | ||||||||
| 치킨 | 0.8 | 0.2 | ||||||||
| 분식 | 0.6 | 0.1 | 0.3 | |||||||
| 피자 | 1.0 | |||||||||
| 운동 | 1.0 | |||||||||
| 만화 | 1.0 | |||||||||
| 잠 | 1.0 |
Episode : 시작상태에서 종결상태에 까지 도달하는 모든 경우의 수
Ep1) 집 → 학교 → 치킨 → 운동 → 잠
Ep2) 집 → 학교 → 치킨 → 잠
Ep3) 집 → 학교 → 분식 → 운동 → 잠
Ep4) 집 → 학원 → 피자 → 만화 → 잠
...
마르코프 보상 과정 (Markov Reward Process)
= 마르코프 연쇄 + 보상(Return)
마르코프 보상 과정은 튜플 data형식으로 표현 가능
(S, P ,R, γ)
- S = 상태의 집합 ex) 집, 학교, 학원, 피자...
- P = 상태 전이 행렬
- R = 보상 함수 (확률적, 결정적일수 있음)
- γ = 감소율? (0 ≤ γ ≤ 1)
보상(Return)
G(t) = 현재시점(t)부터 미래에 예상되는 모든 "할인된 보상"의 합계 (NPV와 비슷한 개념인 듯)
= R(t+1) + γR(t+2) + γ²R(t+3) + ...
※ 보상은 정해진 값이 아닌 확률변수임
가치함수 V(St) = 현재 상태 St에서 보상(Return)의 기대값 E(Gt)
[벨만 항등식 bellman equation]
V(St) = E( G(t) )
= E( R(t+1) + γR(t+2) + γ²R(t+3) + ...)
= E( R(t+1) + γG(t+1) )
= E( R(t+1) + γV(St+1) )
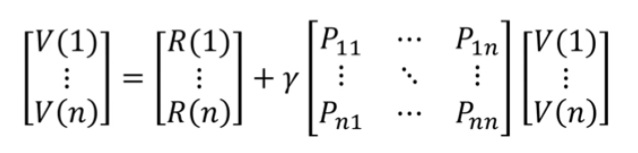
v = R + γPv
(I - γP)V = R (I : 단위행렬)
v = (I - γP)^(-1) R
마르코프 결정과정 (MDP)
- 마르코프 보상과정 (Markov Reward Process)에 행동(A)을 추가
- 마르코프 결정과정은 ( S, A, P, R, γ )인 튜플로 표현 가능
- S = 상태의 집합 ex) 집, 학교, 학원, 피자...
- A = 행동의 집합 ex)
- P = 상태 전이 행렬 => A가 추가됨으로써, 3차원 구조로 표현해야함
- R = 보상 함수 (R : S x A, 확률적/결정적일수 있음)
- γ = 감소율? (0 ≤ γ ≤ 1)
정책함수 π => 어떤 행동을 할 것인가에 대한 기준
- 정책함수 π는 현재 상태(S)에서 수행할 행동들의 확률 분포
- π(a|s) = P(At = a| St = s)
- 강화학습에서는 agent의 현재 상태 St를 이용하여 현재의 행동 At를 결정
※ MDP = π x MRP 의 느낌
MDP에서의 가치함수
- 어떤 상태에서 정책(π)을 따를 때, 얻을 것으로 기대되는 가치의 총합

MDP에서의 행동 가치함수
- 어떤 상태에서 특정 행동을 취하고, 정책(π)을 따랐을 때 얻어질 것으로 기대되는 가치의 총합
- 같은 함수라도 정책π이 달라지면 값이 달라짐
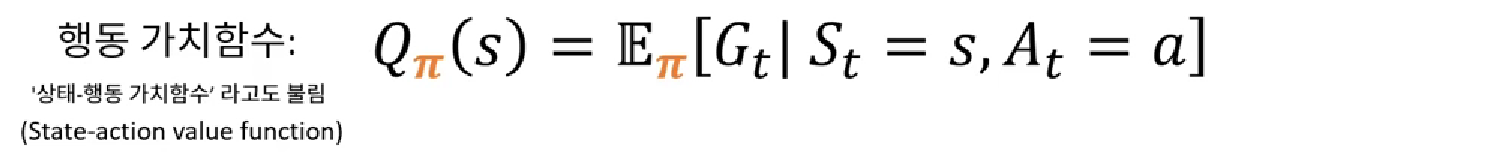
(1)

Σ (행동 가치 함수 x 행동에 대한 기대값)
=> 현재 가능한 모든 행동으로 부터 발생한 기대가치의 가중평균 = 상태 가치 함수
(2)

현재 상태에서 행동 A에 따른 보상 + Σ ( 상태에 도달할 확률 X 상태 가치 함수) * 현재가치 할인
=> 현재 행동 a를 하면 R만큼의 보상을 받고 + 이후 도달할 수 있는 모든 상태(s')로 부터의 기대가치의 합
(2)에 (1)을 대입

좋은 정책함수π의 기준
- 최적 상태 가치 = 모든 상태 (S*)와 모든 정책(π*)을 고려했을 때 얻을 수 있는 가장 높은 상태가치 => V*π(s)
- 최적 행동 가치 = 모든 상태 (S*)와 모든 행동(A*)의 조합 (s, a)과 모든 정책(π*)를 고려했을 때 얻을 수 있는 가장 높은 행동 가치 => Q*π(s, a)
- 최적 정책 π*(a|s) => if a == argmax Q*(s,a)
argmax f(X) = 출력 값 f(x) 을 최대로 만드는 입력 값 (x) 을 반환
max f(x) = 출력 값 f(x)중 최대 값을 반환
벨만 최적 방정식 (Bellman Optimality Equation : BOE)
- 선형 방정식이 아님 => 일반해가 존재하지 않음
- 반복적인 계산을 통해 해를 찾아내야함
- Policy evaluation/ Policy iteration
- Value iteration
- Q-learning
- SARSA ...
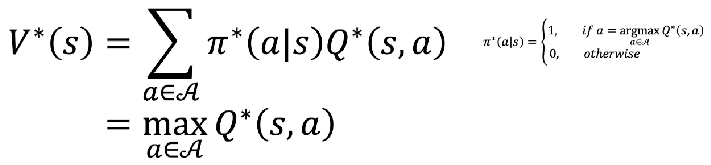


배운내용 되새김질 해보기
마르코프 결정 과정에는
- 상태들이 있음 = S
- 각 상태에서 취할 수 있는 행동들이 있음 = A
- 어떤 행동을 취할지 정하는 기준이 있음 = π
- 마지막으로 각 상태에서 행동을 취했을때 얻어지는 보상이 있음 = R
상태들은 마르코프 연쇄(Markov Chain)를 통해 표현됨
- 상태들의 종류
- 현재 상태에서 다음 상태로 변화할 확률
마르코프 결정 과정(Markov Decision Process)을 배우는 목표
- 주어진 상태들의 조합과 행동의 조합속에서 보상을 최대화 하는, 행동의 기준 (π)을 찾는 것
끝.
'IT > Machine learning' 카테고리의 다른 글
| [ML/강화학습] 강화학습의 기본 이론_ 몬테카를로를 활용한 정책반복 (0) | 2022.10.03 |
|---|---|
| [강화학습] 강화학습 이론_비동기적 동적계획법 (0) | 2022.10.03 |
| [강화학습] 최적의 행동은 어떻게 찾을까? _ 동적계획법 (feat 정책반복) (0) | 2022.10.03 |
| [ML] 머신러닝(Machine learning) 학습 방법_지도학습, 비지도학습, 강화 학습 (2) | 2022.09.30 |
| 머신러닝 vs 딥러닝 (0) | 2020.05.18 |
- Total
- Today
- Yesterday
- 기초
- 시스템투자
- 랜덤맵
- 알고리즘
- 프로그래머스
- 주식투자
- 유니티
- 주식
- 경영학
- requests
- json
- beautifulsoup
- 비전공자
- 강화학습
- 스타트업
- 터틀트레이딩
- 머신러닝
- 심리학
- 파이썬
- 가격데이터
- Anet
- 크롤링
- Unity
- PYTHON
- ET5X
- IT기초
- C#
- It
- 일자별
- 마케팅
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
